y=ax² | g1itec5aee10a

Let´s analise the behaviour of the graphics for the diferent values of a.

When a>0 we have the following examples:

If f(x)= 0.5x²

If g(x)= 4x²

All the parables of these graphics have characteristics in common:

Vertex (0.0)

Concavity facing up

When a<0 we have the following examples:

If f(x)= - 0.5x²

If g(x)= - 4x²

All the parables of these graphics have characteristics in common:

Vextex (0,0)

Concavity facing down

In all this analysis we obtain the following information:

The sinal of a influences the direction of concavity
The value of a influences the opening of the parable. The higher your absolute value less its opening
All these parables have vertex at the point (0.0) and the symmetry is the line x = 0, we can conclude that are independent of a.

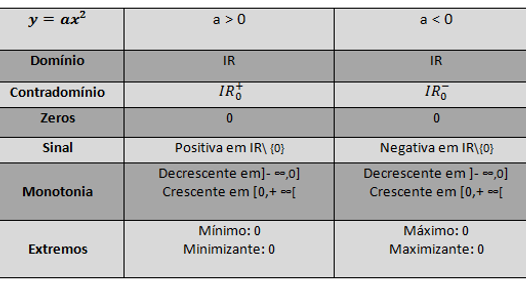
Família de funções do tipo y=ax²; a≠0 | Family functions type y=ax²; a≠0

Vamos analisar o comportamento dos gráficos para diferentes valores de a .

Quando a>0 temos os seguintes exemplos:

Se f(x)= 0.5x²

Se g(x)= 4x²

Todas as parábolas destes gráficos têm características em comum:

Vértice(0,0)

Concavidade voltada para cima

Quando a<0 temos os seguintes exemplos:

Se f(x)= - 0.5x²

Se g(x)= - 4x²

Todas as parábolas destes gráficos têm características em comum:

Vértice (0,0)

Concavidade voltada para baixo

De todas estas análises obtemos as seguintes informações:

O sinal de a influencia o sentido da concavidade
O valor de a influencia a abertura da parábola. Quanto maior o seu valor absoluto, menor a sua abertura
Todas estas parábolas tem vértice no ponto (0,0) e o eixo de simetria é a reta x=0,podemos concluir que são independentes de a.