iTec5
Equipa 1 / Team 1
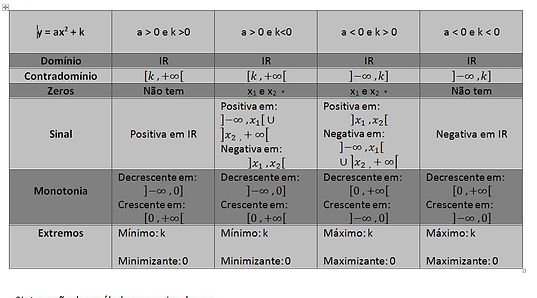
Família de funções do tipo y=ax²+k; a≠0 | Family functions type y=ax²+k;a≠0
*Interseção da parábola com o eixo dos xx
Consider some examples:
If a = 1 and k = 3, we obtein y = x² + 3
If a = 1 and k = - 2, we obtein the function y = x² – 2
Graphic representation:
The graph of the function y = x² + 3 is obtained from the graph of
y = x², displacing the graph three units up (he ordered suffer an additional three units).
The graph of the function y = x² – 2 is obtained from the graph of
y = x², displacing him one unit down (the ordered suffer a decrease of one unit).
The effects of changes of parameter k, on the graphs of the functions of the family y= ax² + k; a 0, make it self felt on the location of the vertex of the parable on the ordinate axis.
Vertex: (0 , k)
Symmetry axis: x = 0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
Considerem-se alguns exemplos:
Se a = 1 e k = 3, obtém-se y = x² + 3
Se a = 1 e k = - 2, obtém-se a função y = x² – 2
Representação gráfica:
O gráfico da função y = x² + 3 obtém-se a partir do gráfico de
y = x², deslocando-o três unidades para cima (as ordenadas sofrem um acréscimo de três unidades).
O gráfico da função y = x² – 2 obtém-se a partir do gráfico de
y = x², deslocando-o uma unidade para baixo (as ordenadas sofrem um decréscimo de uma unidade).
Os efeitos das mudanças de parâmetro k, nos gráficos das funções da família y= ax² + k; a 0, fazem-se sentir na localização do vértice da parábola sobre o eixo das ordenadas.
Vértice: (0 , k)
Eixo de simetria: x = 0
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|
|