iTec5
Equipa 1 / Team 1
Família de funções do tipo y=a (x-h)²; a≠0 | Family functions type y=a(x-h)² ;a≠0
Consider the following functions:
y = x²
y = ( x - 2 ) ²
y= ( x + 3 ) ²
To obtain the graph of the function y = ( x – 2 )² is obtained if the graph of the function y = x² shifted the two units to the right.
To obtain the graph of the function y = ( x + 3 ) ² we obtained first the grafic y = x² shifted trhee units to the left.
If a = -1 e h = -2 we obtain the graph y = - (x + 2)² . The parameter a influences the direction of the concavity of the parable and the opening. The parameter h in this type of function influence the vertex's location of the parable on the abscissa and the axis of symmetry.
Vertex: (h,0)
Symmetry axis: x=h
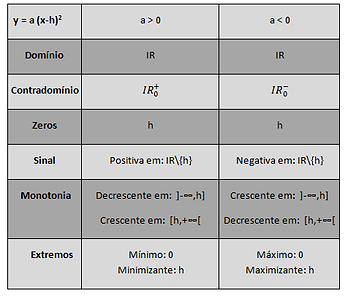
In the table below is a summary of this type of quadratic function:
Considere as seguintes funções:
y = x²
y = ( x - 2 ) ²
y= ( x + 3 ) ²
Para se obter o gráfico da função y = ( x – 2 )² obtém-se o gráfico da função y = x² deslocadondo-o duas unidades para a direita.
Para se obter o gráfico da função y = ( x + 3 ) ² obtemos primeiro o gráfico y = x² deslocadondo-o três unidades para a esquerda.
Se a = -1 e h = -2 obtém-se a função y = - (x + 2)² . O parâmetro a influencia o sentido da concavidade da parábola e também a sua abertura. O parâmetro h neste tipo de funções influência a localização do vértice da parábola sobre o eixo das abcissas e o eixo de simetria.
Vértice: (h,0)
Eixo de simetria: x=h
Na tabela abaixo encontra-se o resumo deste tipo de função quadrática: